矩阵与线性变换
明明线代已经考完了,笔者现在才重新在几何理解线代,属实有点奇怪。
今天在b站的3Blue1Brown听他的线性代数本质,清晰了许多。
很遗憾,矩阵是什么是说不清的,你必须得自己看看。——墨菲斯
矩阵与向量相乘
首先,我们可以知道,直角坐标系中,任意一个向量可以用两个最基本的正交基向量表示,而将两个向量变换(不改变原点位置,直线仍然是直线,对应平行线依旧平行)后的位置,他们坐标会发生变化,相应的,他们所构成的向量也会发生变化。
事实上,我们想要知道变换后的向量的坐标,我们只需要变换后的基向量的坐标和他们之间的几何关系就可以求得。
而变化后的基向量的坐标(3,-2)(2,1)组成一个矩阵,而原线性关系为(5,7),具体可看下面的图片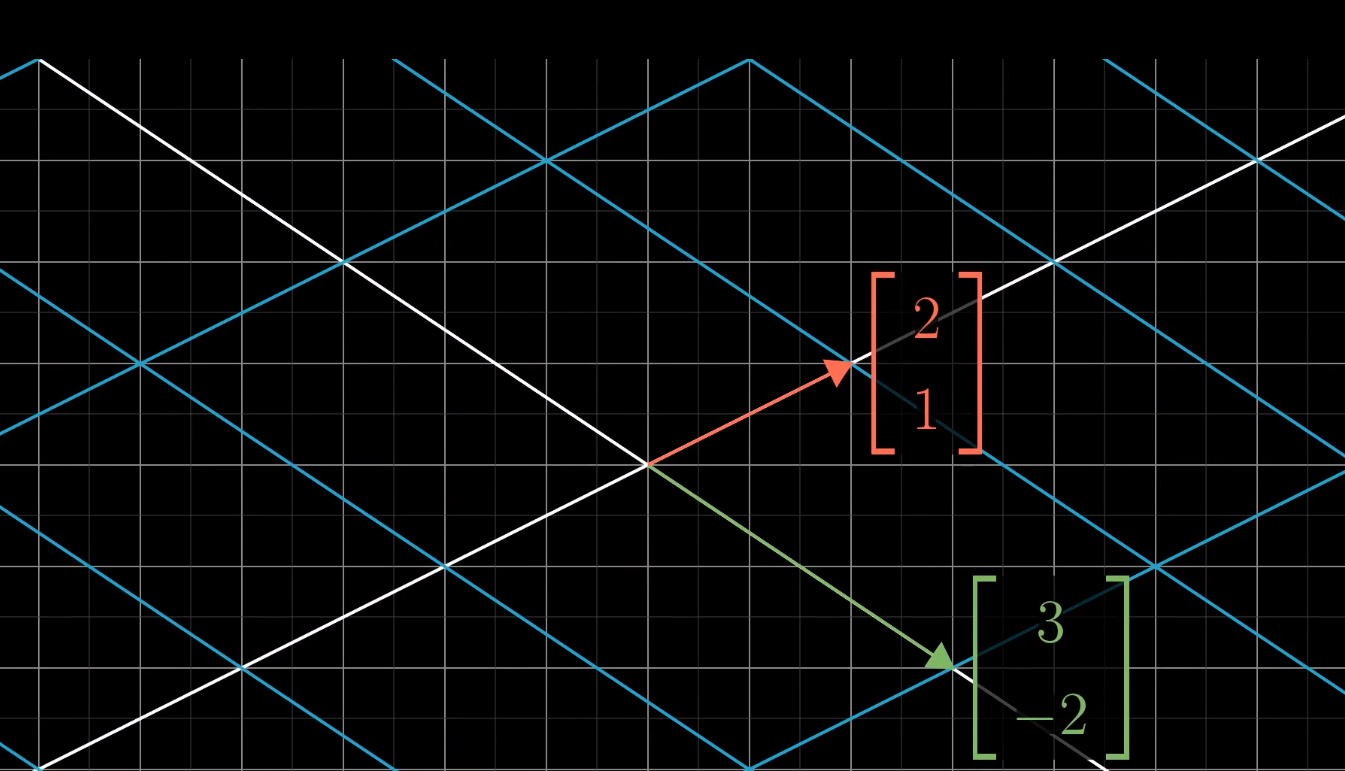
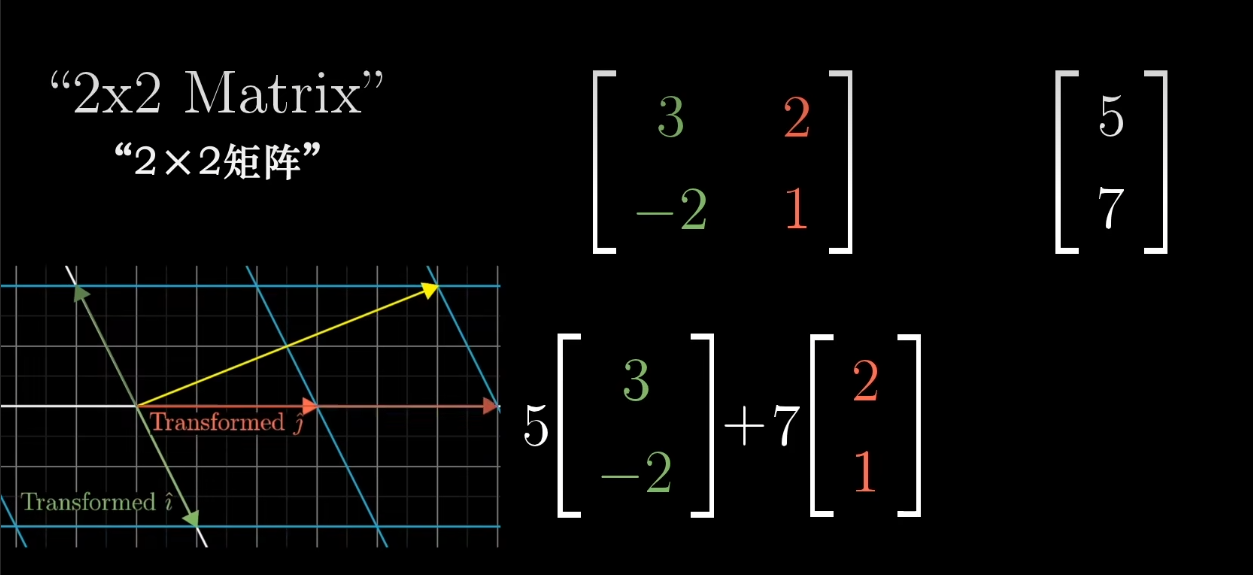
将其抽象出来,我们可以得到矩阵乘于向量的几何含义,就是通过这样的运算得到所构成向量的新坐标。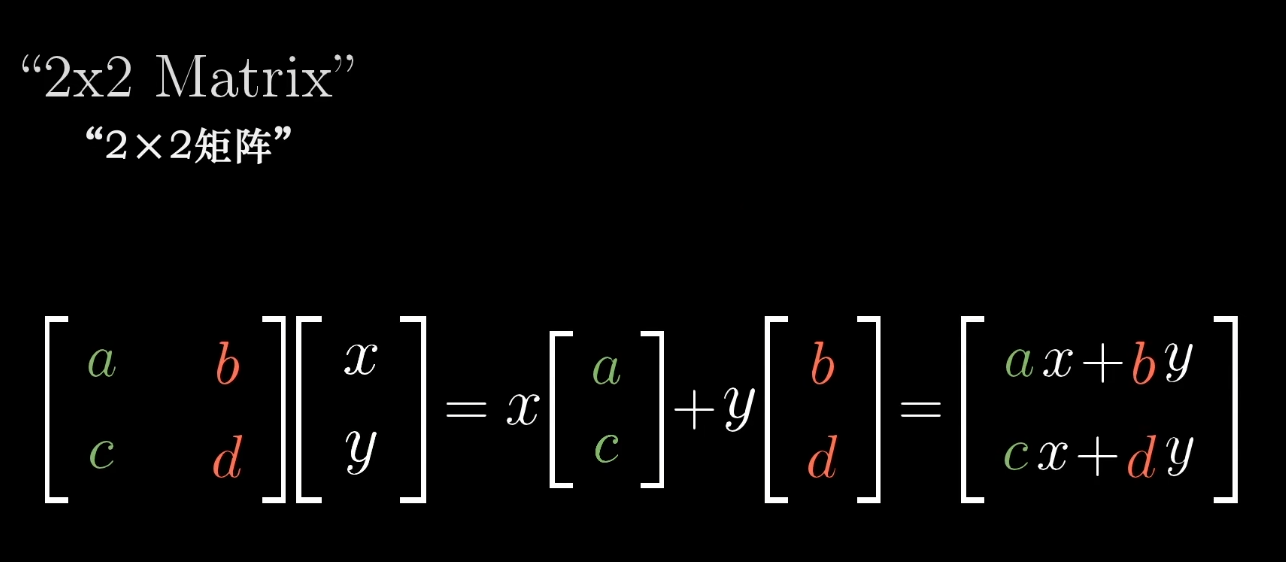
矩阵矩阵相乘
在了解过上面矩阵与向量相乘的几何意义后,我们可以进一步理解矩阵与矩阵相乘的几何意义
在矩阵与矩阵相乘时,我们是要从右边的矩阵看到左边的矩阵,右边的矩阵可以看作若干个向量所构成的矩阵,然后这个向量以左边矩阵的变化。即相当于原来最初的基向量先变成右边矩阵的形式,在分别每列进行左边矩阵的变换。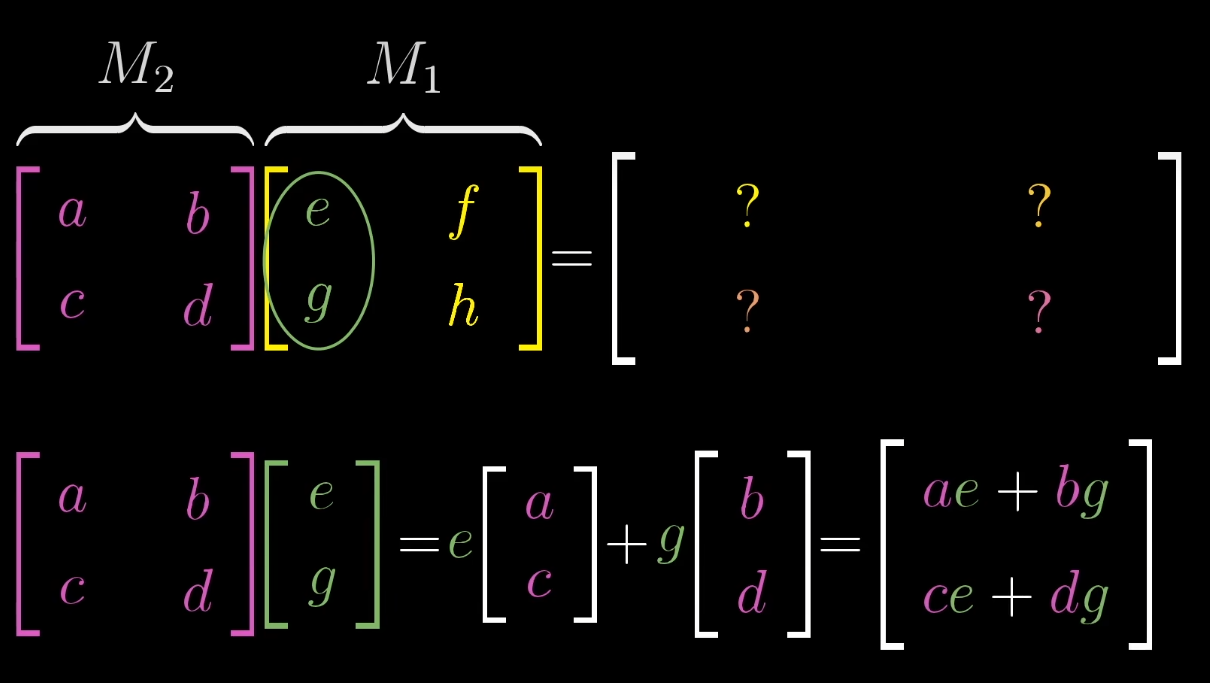
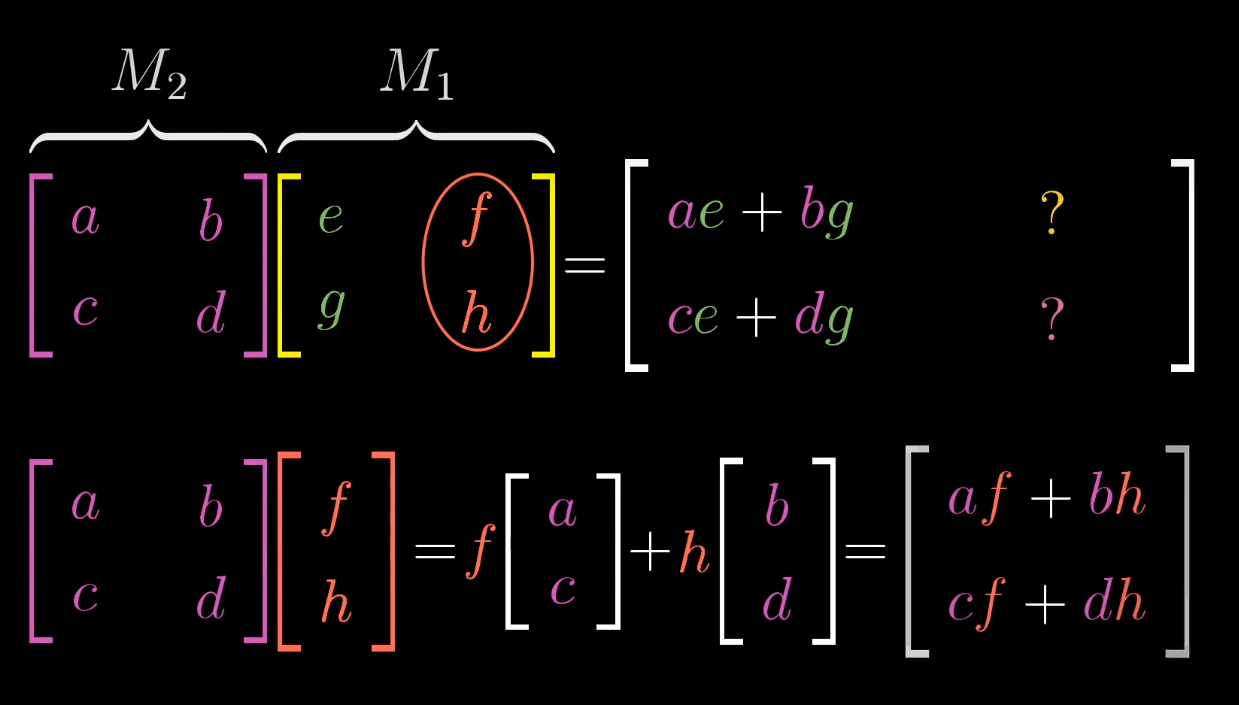
矩阵与线性变换
https://blog.phlin.top/2024/01/24/linear_transformation/